Introduction
The Raspberry Pi is a small-format computer that can run a number of general purpose operating systems, the most popular of which is a build of Linux.
Most computers have relatively poor in-built timekeeping. A time server reads a reference clock and distributes that information over a network. Most computers that have an internet connection regularly synchronize from a publicly accessible timeserver over the internet without the user even knowing.
Accurate timekeeping is important for a number of computing applications; for amateur radio operators using digital modes like JT-X, it is essential to the correct operation of the mode. This blog post explains how I used a cheap GPS chip and Raspberry Pi to serve time to my home network.
Choosing the GPS Chip
The global positioning system is familiar to many as a constellation of orbiting satellites that provides positioning information, but at the heart of each satellite is an atomic clock – the entire system works by comparing slight differences in the time it takes signals from 3 or more satellites to reach a receiver. If you can pick up a signal from a GPS satellite, you have the output from a precise atomic clock, and this can be used to “discipline” (synchronize) your timekeeping.
Most GPS chips pass a message every second containing positioning, diagnostic and timing information. Because this message always arrives slightly (and unpredictably) late, some GPS chips can also supply another channel that pulses to precisely mark the beginning of every second (pulse-per-second, or PPS), a bit like the “pips” on the radio. Obviously the two sources of information need to be combined, as the PPS doesn’t tell the time or date, only the beginning of each second.
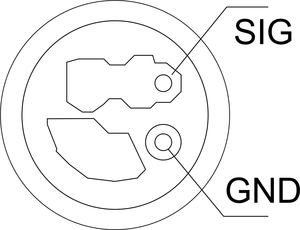
You will need a GPS chip that has a serial output, and ideally a pulse-per-second (PPS) output. I used a very cheap (£7 delivered) board from China called a “Beitian BS-280”, which has an integral antenna and a U-BLOX G7020-KT GNSS receiver. It has 6 I/O connections:
- Tx: TRANSMIT, the channel on which serial data is transmitted from the GPS to the Raspberry Pi
- Rx: RECEIVE, the channel on which serial data is received by the GPS from the Raspberry Pi
- GND: GROUND connection
- VCC: POWER connection for the GPS, typically 5v
- PPS: PULSE-PER-SECOND timing signal
- U.FL: optional external antenna connection
Initial Configuration of the Raspberry Pi
I’ll assume a certain familiarity with Raspberry Pi and/or Linux, so I will refrain from offering a complete step-by step guide to the initial configuration of the Raspberry Pi, as there are many guides available on the internet. I will say that I installed a minimal version of Rasbian 10 (Buster), expanded the filesystem, configured a WiFi connection to my home network using wpa_supplicant and ran the usual updates. The entire configuration was performed via a remote SSH connection.
Connecting the GPS Chip
Firstly, make the following connections between the Raspberry Pi and the GPS:
- RasPi Pin 10 <-> GPS Tx
- RasPi Pin 8 <-> GPS Rx
- RasPi Pin 4 <-> GPS Vcc
- RasPi Pin 6 <-> GPS Gnd
- RasPi Pin 7 <-> GPS PPS
Remember to position your GPS antenna somewhere it can receive a signal – normally with a direct line-of-sight to a sky view. My GPS receiver performs very well in the loft, with the antenna facing the sky.
Next we need to configure the Raspberry Pi to listen to the GPS on the serial interface. By default the Raspberry Pi has a terminal setup on those pins, so we need to run sudo raspi-config and enable to serial connection, and disable the serial console. You can check the interface is now working by running cat /dev/serial0 or cat dev/ttyS0. You should see NMEA formatted data. If you see new data appearing every second, everything is working.
Next we must check that the PPS signal is working correctly. On my unit, the PPS signal is also linked to a LED on the unit, so it is easy to tell when a PPS signal is being produced. To check it is being received:
- Install software using
sudo apt-get install pps-tools. - Add the line
dtoverlay=pps-gpio,gpiopin=4 to the bottom of /boot/config.txt. - Reboot, and check the output of
sudo ppstest /dev/pps0; you should see a line every second.
Setup Timeserver Software
Disable NTP in DHCP
In order to run the Raspberry Pi as a timeserver, we first need to stop it trying to look for another timeserver to syncronise with!
- Remove
ntp-servers from /etc/dhcp/dhclient.conf. - Delete
/lib/dhcpcd/dhcpcd-hooks/50-ntp.conf
Install GPSD
Next we install the software that parses the information from the GPS chip and makes it accessible for the time server software.
sudo apt-get install gpsd-clients gpsd- Edit
/etc/default/gpsd as follows:
# /etc/default/gpsd
#
# Default settings for the gpsd init script and the hotplug wrapper.
# Start the gpsd daemon automatically at boot time
START_DAEMON="true"
# Use USB hotplugging to add new USB devices automatically to the daemon
USBAUTO="false"
# Devices gpsd should collect to at boot time.
# They need to be read/writeable, either by user gpsd or the group dialout.
DEVICES="/dev/serial0 /dev/pps0"
# Other options you want to pass to gpsd
#
# -n don't wait for client to connect; poll GPS immediately
GPSD_OPTIONS="-n"
- Now the moment of truth – test it with
gpsmon. You might need to use set term=vt100 if it looks odd. This should display both GPS position (latitude and longitude),and a number next to “PPS”. - It needs to be setup to boot at background, so use:
systemctl daemon-reloadsystemctl enable gpsdsystemctl start gpsd
- Test the system by rebooting and immediately checking
sudo ntpshmmon. You should see the two sources.
Setup the Time Server
- Check that both time sources are being seem in
sudo ntpshmmon. - Install NTP with
sudo apt-get install ntp. - Modify
/etc/ntp.conf by adding the lines:
# GPS PPS reference
server 127.127.28.2 prefer
fudge 127.127.28.2 refid PPS
# get time from SHM from gpsd; this seems working
server 127.127.28.0
fudge 127.127.28.0 refid GPS
- Restart with
systemctl restart ntp. - Check with
ntpq -p. Please note, if you run this command a few times for the course of an hour or so, you’ll see things change quite a bit. - Eventually, you’ll want to see the PPS (
.SHM.) as the * (selected for synchronization), probably the GPS removed (x or -) and a few random servers in the mix (+) as well. There’s lots of information out there on how ntp decides what the time is by combining multiple sources.
Use the Timeserver
Having a timeserver on the network isn’t much use if your computers don’t know its there! On some network routers with DHCP you can define the server using the internal IP Address (you should also bind the MAC address of the Raspberry Pi to a fixed IP address!), or you can define the address of the server in your operating system settings.